【应用技术】 ZAF校正定量分析数据解析
发表时间:2025-05-20 点击次数:703 关键词:校正定量分析 检测 偏差 相关产品:高分辨型电子显微镜

应用技术部提供一篇EPMA的文章: ZAF校正定量分析数据解析
EPMA的定量分析使用校正程序的目的,是将检测到的X射线的计数转化成检测元素质量分数。由于样品与标样的物理性质不同,检测强度计算出的估计值可能与真实浓度存在差异,需通过校正程序对原始数据进行处理,从而将测量的X射线强度比转换为精 确的元素浓度。文章从以下几个方面进行说明:ZAF校正的基本假设,ZAF校正因子的迭代计算过程,原子序数效应因子的计算,吸收因子的计算,荧光效应因子,计算结果偏差的原因。
文章具体内容如下:
ZAF 校正定量分析数据解析
一、引言 EPMA 的定量分析使用校正程序的目的,是将检测到的 X 射线的计数转化成检测元素质量分数。1951 年 Castaing 在他的博士论文中介绍了他设计的电子探针,并发现电子探针检测出的特征 X 射线比约等于元 素的质量分数比,利用这个原理可以计算出检测元素质量分数的估计值𝑲𝒓𝒂𝒕𝒊𝒐:
𝐶𝑢𝑛𝑘 ≅ 𝐾𝑟𝑎𝑡𝑖𝑜 = 𝐼𝑢𝑛𝑘 𝐼𝑠𝑡𝑑 × 𝐶𝑠𝑡𝑑
其中𝐼𝑢𝑛𝑘是未知样品检测到的特征 X 射线强度,单位计数/(nA×ms);𝐼𝑠𝑡𝑑是标准样品的特征 X 射线强 度;𝐶𝑠𝑡𝑑是标准样品检测元素的质量百分含量。这个过程较正了探测器在探测不同元素的效率差异,但 由于样品与标样的物理性质不同,检测强度计算出的估计值可能与真实浓度存在差异,具体表现为以下三 种效应:
① 原子序数效应:样品与标样组成元素不同,会导致特征 X 射线产额不同;
② 吸收效应:X 射线产生后,穿过样品时会被吸收,导致检测到的特征 X 射线强度降低,样品与标 样的吸收因子不同,会导致吸收额不同;
③ 荧光效应:如果样品中一种元素的特征 X 射线的能量略大于第 二种元素吸收边的能量,则特征 X 射线会发生强吸收。吸收元素被激发在返回基态时会发射特征 X 射线,这会导致一种元素的含量被高估。 样品与标样吸收边的性质不同、二次荧光的激发概率不同,会导致检测到的特征 X 射线强度不同。为消除 以上影响,需通过校正程序对原始数据进行处理,从而将测量的 X 射线强度比转换为精 确的元素浓度。
二、ZAF 校正的基本假设 ZAF 校正是假设样品在分析区域内成分单一且均匀、表面光滑无氧化层的条件下,建立一个探测到的 计数比(X 射线的强度比)与元素浓度的映射关系。要将特征 X 射线强度还原成浓度。
三、ZAF 校正因子的迭代计算过程 根据 Borm所说,一个元素的校正因子𝐺𝐸是所有元素浓度𝐶1 𝑖~𝐶𝑗 𝑖的函数。又由于初始的元素浓度估计 值并不是元素浓度的真实值,因此用第 一估计值计算产生的校正因子必然不能将元素浓度校正为真实值。 第 一次校正得到的元素浓度又可以产生一组新的校正因子,如此反复迭代计算,zui终元素浓度估计值的震 荡,将收敛于一个可接收的范围,此时就得到了一个校正模型的物理假设条件下存在一个唯 一的元素浓 度自洽解。这个解不能保证与真实元素浓度相同,校正结果的准确度取决于物理模型的假设是否与实际情 况相符。在实际分析中,迭代次数(图一中 Iteration 值)反映了计算的收敛过程。
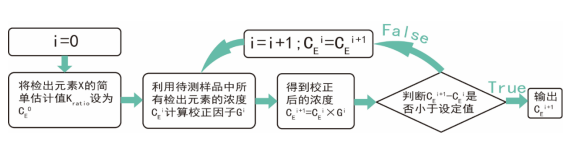
图二 ZAF 校正因子迭代计算的过程
ZAF 校正的工作流程如图二所示。为了获得校正因子𝐺𝐸 𝑖 ,首先,测量未知样品产生的所有特征 X 射 线,并识别组成样品的一系列元素 X。将测得的𝐾𝑟𝑎𝑡𝑖𝑜设为元素的第 一近似浓度𝐶𝐸 0(即检测元素的初步质 量分数)。然后,利用未知样品中所含所有组成元素的第 一近似浓度𝐶𝑥 𝑖计算出校正因子𝐺𝐸 0。将𝐶𝐸 0乘以𝐺𝐸 0计 算出第 二近似质量浓度𝐶𝐸 1。接下来,按照同样的步骤利用校正后的质量浓度𝐶𝐸 1,求出𝐺𝐸 1,并将𝐶𝐸 1乘以 𝐺𝐸 1,计算出𝐶𝐸 2。重复此过程,当计算出的质量浓度差𝐶𝐸 𝑖+1 -𝐶𝐸 𝑖小于设定的可接受的误差值(例如 0.001%) 之后,输出𝐶𝐸 𝑖+1为校正后的元素浓度估计值,输出𝐺𝐸 𝑖+1为校正因子。
四、原子序数效应因子𝑮𝑬 𝒁的计算 如前文所述使用 ZAF 校正是建立一个探测到的计数比(X 射线的强度比)与元素浓度的映射关系。原 子序数效应因子𝐺𝐸 𝑍建立了一个被电子束直接激发的特征 X 射线强度 IE与元素浓度 C 之间的映射关系。激 发特征 X 射线所需的能量,来源于入射电子束的与样品原子发生弹性散射损失的能量,Bethe将这种集体 效应总结为电子束在样品内一种连续的能量损失,并将单位质量下的能量损失定义为了阻止能力 S。
背散射因子 R 则是为了修正由于在电子耗尽其电离能力之前,因弹性散射提前离开样品,导致电离事 件减少。平均原子序数越大背散射出样品的电子数量越多,而发生非弹性散射的对 X 射线产生有贡献的电 子数量越少(图三)。
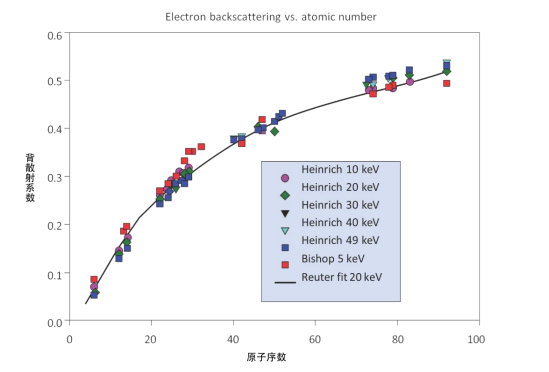
图三 背散射系数和原子序数的关系
(背散射系数是背散射电子的数量与入射电子的数量之比)
五、吸收因子𝑮𝑬 𝑨的计算 特征 X 射线在样品中传播时可能被样品吸收,因此实际检测到的 X 射线强度 I 并不是 X 射线产生时的强度 I0,吸收因子𝐺𝐸 𝐴建立了 I 与 I0之间的映射关系[2]:𝐼 = 𝐼0 × 𝑓(𝜀)。X 射线的吸收额与其吸收程 x 以及 样品的质量吸收系数(μ/ρ)相关(图四),吸收程可以由激发深度 h 与取出角Ψ写出:𝑥 = ℎ × 𝑐𝑜𝑠𝑒𝑐𝜓;而激 发深度又与入射电子能量 E0 以及测试元素的临界激发能 Ec有关,最终吸收因子可以写成一个与ε=(μ/ρ)× 𝑐𝑜𝑠𝑒𝑐𝜓和 E0、Ec 的函数。吸收因子是三个因子中对定量结果影响最大的因子。
质量吸收系数 μ/ρ,是物质的固有属性,与物质的状态无关。只要 X 射线穿透的区域是均匀的,物质 的吸收系数都可以用组成物质的元素浓度以及元素的质量吸收系数线性加和求得。假设物质由 A、B、C 三种元素组成,它们的浓度依次是 CA、CB、CC,三种元素的质量吸收系数是(μ/ρ)A、(μ/ρ)B、(μ/ρ)C,物质 的整体的质量吸收系数为(μ/ρ)=CA(μ/ρ)A+CB(μ/ρ)B+CC(μ/ρ)C。质量吸收系数既包含了物质对 X 射线的光电 吸收(表现吸收边吸收系数的突变)也包含了散射吸收,吸收系数来源于计算使用的数据库。
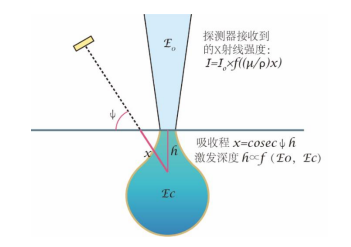
图四 特征 X 射线的吸收过程
当样品中特征 X 射线的能量足够高时,X 射线还有可能再次电离样品中的低临界激发能元素,因此对 于产生的特征 X 射线总强度 I0 实际上包含了一次激发产生的特征 X 射线强度 IE 以及二次激发事件产生的 特征 X 射线强度 IF(二次激发对应的能量吸收过程已经包含于吸收因子的光电吸收部分),而与物质浓度 相关的只有一次激发产的特征 X 射线强度 IE。
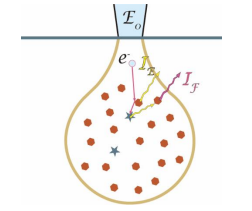
图五 由电子束激发的特征 X 射线,以及由连续 X 射线和特征 X 射线激发的二次荧光 X 射线
七、计算结果偏差的原因 ZAF 校正后的结果与 100%之间的偏离程度,既反映了 ZAF 校正的物理模型与现实情况的偏离程度, 也会受到外部条件的影响。最常见的影响来自于扣除背底后的计数率不足(net 值过小)或未在校正时检 出所有已知元素,当偏离值较大时结果甚至可能不如第一近似值𝑲𝒓𝒂𝒕𝒊𝒐更具有参考意义。
免责声明:本平台文章均系转载,版权归原作者所有。所转载文章并不代表本网站赞同其观点和对其真实性负责。如涉及作品版权问题,请及时联系我们400-099-6011,我们将作删除处理以保证您的权益。
上一篇:2025年度北京波谱
下一篇:荣耀加冕|欧波同蝉
与此资讯相关条目
热点新闻推荐



